Solution :
The relationship between the strength of magnetic field and the radiusof a charged particle's path is obtained through Newton's second law, which is given by :
F = ma
F = qvB and
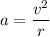
Substituting these values in the second law of Newton,
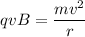
Now solving for B, we get:
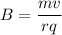
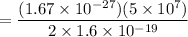
= 0.261 T
The field strength can be obtained by using the technology of today.