Answer:
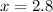
or

I chose the quadratic formula because I could not factor the quadratic.
Explanation:
First of all let's work out what
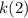 equals to. We can do this by replacing every
equals to. We can do this by replacing every
 term in
term in
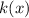 with a 2.
with a 2.
So:
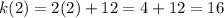
Now let's set up our equation
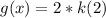 . Replace the functions with what we know they equal to.
. Replace the functions with what we know they equal to.
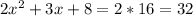
Now bring all the terms to one side:

Now we can solve this quadratic for
 .
.
I'll put this into the quadratic formula because it cannot be factored.
 , Compare our quadratic to the general equation of a quadratic:
, Compare our quadratic to the general equation of a quadratic:
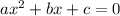 .
.
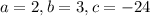
Now put these terms into the quadratic formula to get the values for
 .
.
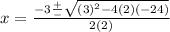
So:
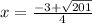 =2.8 (1 decimal place)
=2.8 (1 decimal place)
or
 = -4.3 (1 decimal place)
= -4.3 (1 decimal place)