Question

24

,
Factor:
x²-9
A
(x + 3XX-3)
B
(x+3)2
с
(x-3)
(x+3)(x+3)

Answer 1

(x-3)(x+3)

Explanation:

We are given the expression
`\displaystyle \large{x^2-9}`:—

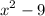To factor this expression, we have a formula for it which is difference of two squares:—

`\displaystyle \large{a^2-b^2=(a+b)(a-b)}`

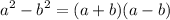
You can also swap from
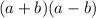`\displaystyle \large{(a+b)(a-b)}` to
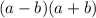`\displaystyle \large{(a-b)(a+b)}` via multiplication property.

From the expression, factor using the formula above:—

`\displaystyle \large{x^2-9=(x^2)-(3)^2}\\\displaystyle \large{x^2-9=(x-3)(x+3)}`

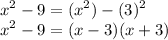
Therefore, the factored expression is:—

`\displaystyle \large{\boxed{(x-3)(x+3)}}`

__________________________________________________________

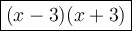
If you have any questions regarding the problem or need clarification of my answer/explanation, do not hesitate to ask in comment!