Question

Assume that body masses of Goldfinch birds follow a normal distribution with standard deviation equal to 0.04 oz. An ornithologist would like to make some inference about the average body mass of Goldfinch birds. In particular, she would like to create a formula to compute 70 % confidence interval formula for the average body mass of this specie. Her equipment allows her to sample 10 birds, using the 10 independent measurements CREATE the formula to generate 70% confidence intervals. Explain the crucial steps.

Answer 1

The formula to generate 70% confidence interval is:
`[\overline{x} - 0.013, \overline{x} + 0.013]`, in which
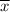`\overline{x}` is the sample mean.

Explanation:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.7)/(2) = 0.15`

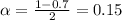
Now, we have to find z in the Z-table as such z has a p-value of
`1 - \alpha`.

That is z with a pvalue of
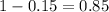`1 - 0.15 = 0.85`, so Z = 1.037.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

Assume that body masses of Goldfinch birds follow a normal distribution with standard deviation equal to 0.04 oz.

This means that
`\sigma = 0.04`.

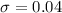Sample of 10 birds:

This means that
`n = 10`.

The margin of error is of:

`M = z(\sigma)/(√(n))`

`M = 1.037(0.04)/(√(10))`

`M = 0.013`

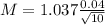
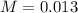
The lower end of the interval is the sample mean of
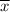`\overline{x}` subtracted by M.

The upper end of the interval is the sample mean of
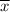`\overline{x}` added to M.

Then, the formula to generate 70% confidence interval is:
`[\overline{x} - 0.013, \overline{x} + 0.013]`, in which
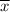`\overline{x}` is the sample mean.