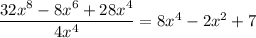Question

Divide the following polynomials and then complete the quotient. Write your answer in order of decreasing powers of x.

(32x^8-8x^6+28x^4)÷4x^4=

Answer 1

The answer is 4 I think

Answer 2

The division of the polynomial is
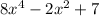`8x^4 - 2x^2 + 7` and the complete quotient is
`(32x^8-8x^6+28x^4)/(4x^4) = 8x^4 - 2x^2 + 7}`

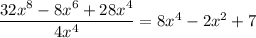
How to divide the polynomials

From the question, we have the following parameters that can be used in our computation:

`(32x^8-8x^6+28x^4)/(4x^4)`

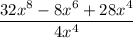
Factor out 4 from the numerator

So, we have

`(32x^8-8x^6+28x^4)/(4x^4) = 4 * (8x^8 - 2x^6 + 7x^4)/(4x^4)`

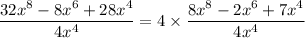
Evaluate the quotient

`(32x^8-8x^6+28x^4)/(4x^4) = (8x^8 - 2x^6 + 7x^4)/(x^4)`

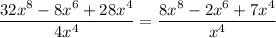
Factor out x⁴ from the numerator

`(32x^8-8x^6+28x^4)/(4x^4) = x^4 * (8x^4 - 2x^2 + 7)/(x^4)`

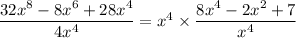
Evaluate the quotient

`(32x^8-8x^6+28x^4)/(4x^4) = 8x^4 - 2x^2 + 7`

Hence, the division of the polynomial is
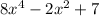`8x^4 - 2x^2 + 7` and the complete quotient is
`(32x^8-8x^6+28x^4)/(4x^4) = 8x^4 - 2x^2 + 7}`