Question

Bet u can’t solve this

Answer 1

Explanation:

Assuming you're solving for p:

`m=2^(-1) *2^p(2^p-1)`

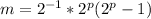
Let
`y=2^p`

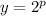
Now we can re-write the equation with
`y` instead of
`2^p`.

`m=(1)/(2) y(y-1)`

`2m=y^2-y`

`y^2-y-2m=0`

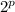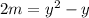
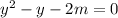
Use the quadratic formula to get:

`y = (1+√(1+8m) )/(2)`

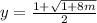
or

`y = (1-√(1+8m) )/(2)`

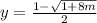
Therefore, using natural log and log rules:

`2^p = (1+√(1+8m) )/(2)`,
`ln(2^p)= ln((1+√(1+8m) )/(2))`,
`pln(2) = ln((1+√(1+8m) )/(2))`,
`p = (ln((1+√(1+8m) )/(2)))/(ln(2))`

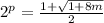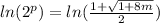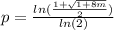
or

`2^p = (1-√(1+8m) )/(2)`,
`ln(2^p)= ln((1-√(1+8m) )/(2))`,
`pln(2) = ln((1-√(1+8m) )/(2))`,
`p = (ln((1-√(1+8m) )/(2)))/(ln(2))`

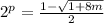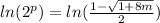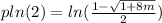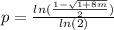
If I haven't made any mistakes this should be correct!