Question

A lidless box is constructed by cutting a square with side length x from a rectangular sheet of paper with dimensions a x b. After the cut is removed, the sides are folded up to form the

box.
a) Find the value of x (in terms of a and b) that maximizes the volume of the box.
b) Find the value of x that maximizes the volume of the box when a = 8.5 inches and b= 11 inches.

Answer 1

a)
`x =(a+b -√((a + b)^2 - 3\cdot a \cdot b) )/(6)`

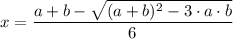
b) The volume of the box is maximized when 'x' is approximately 1.585 feet

Explanation:

a) Let 'a' represent the length of the rectangular sheet of paper and let 'b' represent the with of the rectangular sheet of paper, we have;

The length of the side of the square cut from the corners of the rectangular sheet of paper = x

The length of the box formed after cutting the square sides are;

The length of the box, l = a - 2·x

The width of the box, w = b - 2·x

The height of the box, h = x

The volume of the box, V = l × w × h = (a - 2·x)·(b - 2·x)·x = 4·x³ - 2·a·x² - 2·b·x² + a·b·x

The value of 'x' that gives the maximum volume of the box is given by finding the extremum of the volume, 'V', of the box as follows;

At the extremum, dV/dx = 0

∴ d(4·x³ - 2·a·x² - 2·b·x² + a·b·x)/dx = 12·x² - 4·a·x - 4·b·x + a·b = 0

12·x² - 4·(a + b)·x + a·b = 0

`x = (4\cdot (a + b) \pm √((-4\cdot (a + b) )^2-4 *12* a \cdot b ) )/(2 * 24) =(a+b\pm√((a + b)^2 - 3\cdot a \cdot b) )/(6)`

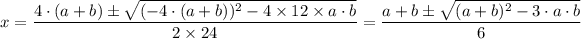
Found from part (b), the value of 'x' (in terms of 'a' and 'b') that maximizes the volume of the box is
`x =(a+b -√((a + b)^2 - 3\cdot a \cdot b) )/(6)`

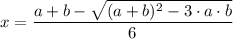
b), When a = 8.5 inches and b = 11 inches, we have;

x = (8.5 + 11 +√((8.5 + 11)² - 3×8.5×11))/6 = 4.914

x = (8.5 + 11 -√((8.5 + 11)² - 3×8.5×11))/6 ≈ 1.585

We get;

When x = 1.585, V = 4·1.585³ - 2·8.5·1.585² - 2·11·1.585² + 8.5·11·1.585 ≈ 66.15

When x = 4.914, V = 4·4.914³ - 2·8.5·4.914² - 2·11·4.914² + 8.5·11·4.914 ≈ -7.65

Therefore, the value of 'x' that gives the maximum volume of the box is x = (8.5 + 11 -√((8.5 + 11)² - 3×8.5×11))/6 ≈ 1.585

(The value of 'x' in terms of 'a' and 'b' is therefore;

`x =(a+b -√((a + b)^2 - 3\cdot a \cdot b) )/(6)`)

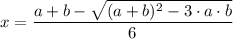The volume of the box is maximized when, x ≈ 1.585 feet