Question

For what value of y does
25-()
25
?

Answer 1

Answer: his is a simple as well as an interesting question. CASE I: y = 25. Consider this a² = |a|. Given y = 25, we can write like this way,. y = -5/2.

Explanation:

Answer 2

-1/2

Explanation:

We are given the exponential equation:—

`\displaystyle \large{125=((1)/(25))^(y-1)}`

First, use a law of exponent [Quotient Rules] to convert RHS:—

`\displaystyle \large{125=(25^(-1))^(y-1)}`

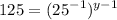
Then convert both bases to base 5:—

`\displaystyle \large{5^3 = (5^(-2))^(y-1)}`

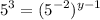
Use another law of exponent [Power] to multiply the exponent of RHS:—

`\displaystyle \large{5^3 = 5^(-2y+2)}`

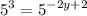
Now that both sides have same base, solve the equations with exponent:—

`\displaystyle \large{3=-2y+2}\\\displaystyle \large{1=-2y}\\\displaystyle \large{y=-(1)/(2)}`

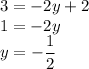
Therefore, the value of y is:—

`\displaystyle \large{\boxed{-(1)/(2)}}`

__________________________________________________________

Summary

This section includes an important or necessary explanation, summary or formulas that was used in the explanation above.

Laws of Exponent

Power of Power Rules:—

`\displaystyle \large{(a^m)^n = a^(mn)}`

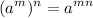
Quotient Rules:—

`\displaystyle \large{a^(-n)=(1)/(a^n)}`

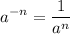
Note that the above, Quotient Rules, is derived from:—

`\displaystyle \large{(a^m)/(a^n) = a^m / a^n = a^(m-n)`

But when m = 0 the numerator becomes 1.

Exponential Equation

When solving an Exponential Equation, the goal is to convert both sides having the same base.

When both sides have same base, take both exponents of both sides to solve the equation.

__________________________________________________________

If you have any questions regarding this problem or need clarification, do not hesitate to ask in comment! Good luck on your assignment and have a nice day!