Question

You are asked to design a spring that will give a 1070 kg satellite a speed of 3.75 m/s relative to an orbiting space shuttle. Your spring is to give the satellite a maximum acceleration of 5.00g. The spring's mass, the recoil kinetic energy of the shuttle, and changes in gravitational potential energy will all be negligible.

(a) What must the force constant of the spring be?
(b) What distance must the spring be compressed?

Answer 1

`380697.33\ \text{N/m}`

`0.138\ \text{m}`

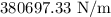
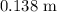
Step-by-step explanation:

m = Mass rocket = 1070 kg

v = Velocity of rocket = 3.75 m/s

a = Acceleration of rocket = 5g

g = Acceleration due to gravity =
`9.81\ \text{m/s}^2`

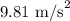
The energy balance of the system is given by

`(1)/(2)kx^2=(1)/(2)mv^2\\\Rightarrow kx=(mv^2)/(x)\\\Rightarrow kx=(1070* 3.75^2)/(x)\\\Rightarrow kx=(7250)/(x)`

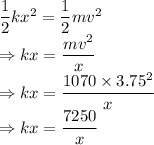
The force balance of the system is given by

`ma=kx\\\Rightarrow m5g=(7250)/(x)\\\Rightarrow x=(7250)/(1070* 5* 9.81)\\\Rightarrow x=0.138\ \text{m}`

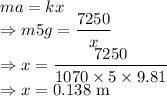
The distance the spring must be compressed is
`0.138\ \text{m}`

`k=(7250)/(x^2)\\\Rightarrow k=(7250)/(0.138^2)\\\Rightarrow k=380697.33\ \text{N/m}`

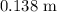
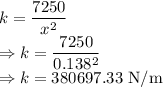
The force constant of the spring is
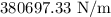`380697.33\ \text{N/m}`.