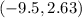Question

Please help serious answers only

Answer 1

`(-9.5,2.63)`

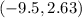
Explanation:

In essence, this problem asks one to find the vertex of the given equation. An easy way to find the vertex of a quadratic equation in standard form is to complete the square.

Completeting the square involves grouping the quadratic and linear term, then factoring out the coefficient of the quadratic term. After doing so, one will add a term to make the grouped terms a perfect square trinomial and then balance the equation. Finally, one will simplify the equation and get the quadratic equation in vertex form. From there, finding vertex is quite easy, the x-coordinate is the additive inverse of the quadratic term, and the y-coordinate is the constant.

Once a quadratic equation in standard form has been converted to vertex form by the process of completing the square, its equation is amongst the lines of the following,

`a(x-k)^2+h`

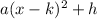
(k, h) is the vertex of the parabola.

The quadratic equation in standard form,

`2x^2+19x+42.5`

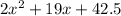
Group the quadratic and linear terms,

`(2x^2+19x)+42.5`

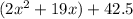
Factor out the coefficient of the quadratic term,

`2(x^2+9.5x)+42.5`

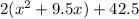
Add a term to make the grouped part a perfect square trinomial, then balance the equation,

`2(x^2+9.5x+22.5625)+42.5-2(22.5625)`

Simplify,

`2(x^2+9.5x+22.5626)+42.5-45.125`

`2(x+9.5)^2+2.625`

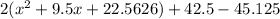
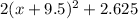
The vertex of the equation is the following,

`(-9.5,2.625)`

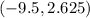
Rounded,

`(-9.5,2.63)`