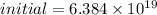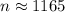Question

Suppose that you must go into court and testify as to the level of X in the river water. Your lawyer is concerned that your analytical results are lower than they should be because you cannot extract with benzene (distribution Ratio K=4) all of X from your samples. Assume the concentration of X in the 1.00 L river water sample is 1.06 x 10-4 M.

a. How many extracts would be required to remove all but 1000 molecules of X from the sample with repeated 10.00 mL portions of extract?
b. How many extractions are required for a 99.99% chance of extraction of the last molecule remaining (0.01% chance of a single molecule left behind)

Answer 1

The appropriate solution is:

(a) n ≈ 900

(b) n ≈ 1165

Step-by-step explanation:

According to the question,

(a)

The final number of molecules throughout water will be:

=
`((1000)/(1000)* 4* 10 )^n`

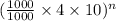
where, n = number of extractions

Now,

The initial number of molecules will be:

=
`1.06* 10^(-4)* 6.023* 10^(23)`

=
`6.387* 10^(19)`

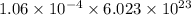
Final number of molecule,

⇒
`1.566* 10^(-16)=((1000)/(1040) )^n`

`n \approx 900`

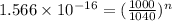
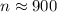
(b)

Final molecules of X = left (0.01%)

hence,

⇒
`initial = 6.384* 10^(19)`

`(1)/(6.384* 10^(19)) =((1000)/(1040) )^2`

`n \approx 1165`