Answer:
In 59 days, the number of bacteria reaches 1000.
Explanation:
Given the data in the question;
by placing 100 spores of the bacteria at the start of the project,
p(0) = 100
dP over dt equals the product of 0.05 times P and the quantity 1 minus P over 2000
dp/dt = 0.05p( 1 - p/200 )
2000dp / p( 2000 - p ) = 0.05dt
[1 / p + 1 / 200-p ]dp = 0.05 dt
Now, we integrate
∫[1 / p + 1 / 200-p ]dp = ∫ 0.05 dt
ln p - ln [2000 - p ] = 0.05 + c'
ln[ p / 2000 - p ] = 0.05 + c'
p / 2000 - p =
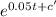
p / 2000 - p = k
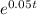
Now, since p(0) = 100, we substitute
100 / (2000 - 100) = k
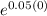
100 / 1900 = k ×
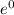
100 / 1900 = k × 1
k = 1 / 19
Therefore,
p / 2000 - p = k
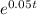
p / 2000 - p = (1/19)
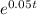
when p( t ) = 1000, then t will be;
1000 / (2000 - 1000) = (1/19)
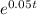
1000 / 1000 = (1/19)
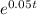
1 = (1/19 ) ×
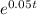
1/(1/19 ) =
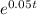
(1 × 19)/1 =
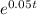
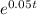 = 19
= 19
0.05t = ln( 19 )
0.05t = 2.9444
t = 2.9444 / 0.05
t = 58.888 ≈ 59 days
Therefore, In 59 days, the number of bacteria reaches 1000.