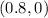Answer:
 -intercepts at
-intercepts at
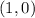 and
and
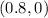
Explanation:
A quadratic in the form
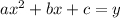 crosses the
crosses the
 -axis when
-axis when
 .
.
The first step is replacing
 with
with
 .
.
So:
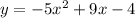 . With the information above, we can find the
. With the information above, we can find the
 intercepts by setting
intercepts by setting
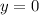 .
.
Therefore
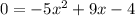 .
.
Now we can use the quadratic formula because it is in the form
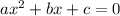 .
.
Note the quadratic formula:
 .
.
To find the values of
 ,
,
 and
and
 we can compare the equation to the general equation.
we can compare the equation to the general equation.
Therefore:
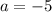 ,
,
 and
and
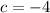 .
.
Now put these values into the quadratic formula:
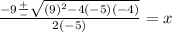
And simplify:
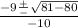 ,
,
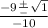 .
.
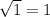 , therefore
, therefore
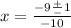
Now we can have two values for
 . One when we take away the discriminant (
. One when we take away the discriminant (
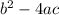 ) and one when we add it.
) and one when we add it.
So
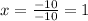
or
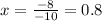
Therefore
 -intercepts at
-intercepts at
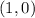 and
and