Answer:
Explanation:
Can't sketch it, obviously, but I can help you understand how to do that on your own. The standard form of a circle is
 where h and k are the coordinates for the center of the circle. The super-important thing to remember here is that the standard form is ALWAYS (x-h)^2 (the minus being the important part!). That means that if the expression is
where h and k are the coordinates for the center of the circle. The super-important thing to remember here is that the standard form is ALWAYS (x-h)^2 (the minus being the important part!). That means that if the expression is
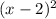 for example, it can be rewritten to be understood as
for example, it can be rewritten to be understood as
 where the positive implies movement to the right. If the expression is
where the positive implies movement to the right. If the expression is
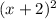 for example, it can be rewritten to be understood as
for example, it can be rewritten to be understood as
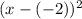 where negative is indicative of movement to the right. The location of the center of a circle will help you graph it.
where negative is indicative of movement to the right. The location of the center of a circle will help you graph it.
In our circle, we have a -1 in with the x and a +3 in with the y. The -1 indicates movement to the right 1 unit (positive 1), while the +3 in with the y indicates movement to the left 3 units (-3). Therefore, the movement of the circle also indicates the coordinates of the center: (1, -3).
The radius is found in the square root of the number to the right of the equals sign. Ours is a 4; therefore, the radius is 2.
To draw this circle, locate the point (1, -3) on your graph paper and put a dot. Then count directly to the right 2 units and make a dot, directly to the left 2 units and make a dot, directly up 2 units and make a dot, and directly down 2 units and make a dot. Connect the outer 4 dots in as smoothly as possible to get a circle. And there you go!