Question

Find an explicit formula for the geometric sequence below.

Answer 1

Explanation:

The formula for an explicit geometric formula (as opposed to a recursive one) is

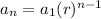`a_n=a_1(r)^(n-1)` where a(n) is representative of the position of a number in the sequence, a(1) is the first number in the sequence, and r is the common ratio. The common ratio is the same number that must be either multiplied in or divided out to get to the next number in the term. Notice that the top numbers in our sequence are doubling which implies we are multiplying the top numbers by -2, and the bottom numbers are going up by multiples of 3. So our common ratio is -2/3. Try it and see:

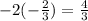`-2(-(2)/(3))=(4)/(3)` and

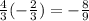`(4)/(3)(-(2)/(3))=-(8)/(9)` etc.

Therefore, the explicit geometric formula for this sequence is

`a_n=-2(-(2)/(3))^{n-1`

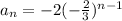
You can use this formula to find any number in the sequence; for example, if you wanted to know the 100th number in this sequence, simply replace n with 100 and do the math. That's what an explicit formula is used for.

Answer 2

see explanation

Explanation:

The nth term ( explicit formula) of a geometric sequence is

`a_(n)` = a₁
`(r)^(n-1)`

where a₁ is the first term and r the common ratio

Here a₁ = - 2 and r =
`(a_(2) )/(a_(1) )` =
`((4)/(3) )/(-2)` = -
`(2)/(3)` , then

`a_(n)` = - 2
`(-(2)/(3)) ^(n-1)` ← explicit formula