Question

Find the center and radius of the circle with equation (x + 9)^2 + (y + 5)^2 = 64

Answer 1

Explanation:

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2` with the really important part being the x- and the y-. If our first set of parenthesis is

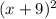`(x+9)^2`, by the definition of the standard form of a circle, it actually is

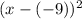`(x-(-9))^2` which is obviously negative (that's the h of the center of the circle);

If our second set of parenthesis is

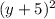`(y+5)^2`, by the definition of the standard form of a circle, it actually is

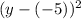`(y-(-5))^2` which is obviously negative (that's the k of the center of the circle). The radius is the square root of the constant on the right, 64. The square root of 64 is 8, so

Center (-9, -5), radius 8