Question

A self-driving car traveling along a straight section of road starts from rest, accelerating at 2.00 m/s2 until it reaches a speed of 25.0 m/s. Then the vehicle travels for 39.0 s at constant speed until the brakes are applied, stopping the vehicle in a uniform manner in an additional 5.00 s.

(a) How long is the self-driving car in motion (in s)?
(b) What is the average velocity of the self-driving car for the motion described? (Enter the magnitude in m/s.) m/s

Answer 1

`56.5\ \text{s}`

`21.13\ \text{m/s}`

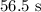
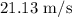
Step-by-step explanation:

v = Final velocity

u = Initial velocity

a = Acceleration

t = Time

s = Displacement

Here the kinematic equations of motion are used

`v=u+at\\\Rightarrow t=(v-u)/(a)\\\Rightarrow t=(25-0)/(2)\\\Rightarrow t=12.5\ \text{s}`

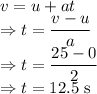
Time the car is at constant velocity is 39 s

Time the car is decelerating is 5 s

Total time the car is in motion is
`12.5+39+5=56.5\ \text{s}`

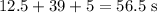
Distance traveled

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2a)\\\Rightarrow s=(25^2-0)/(2* 2)\\\Rightarrow s=156.25\ \text{m}`

`s=vt\\\Rightarrow s=25* 39\\\Rightarrow s=975\ \text{m}`

`v=u+at\\\Rightarrow a=(v-u)/(t)\\\Rightarrow a=(0-25)/(5)\\\Rightarrow a=-5\ \text{m/s}^2`

`s=(v^2-u^2)/(2a)\\\Rightarrow s=(0-25^2)/(2* -5)\\\Rightarrow s=62.5\ \text{m}`

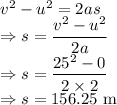
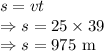
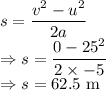
The total displacement of the car is
`156.25+975+62.5=1193.75\ \text{m}`

Average velocity is given by

`\frac{\text{Total displacement}}{\text{Total time}}=(1193.75)/(56.5)=21.13\ \text{m/s}`

The average velocity of the car is
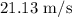`21.13\ \text{m/s}`.