Question

An engineer stands 200 feet from a tower and sights the top of the tower at a 45° angle of elevation. Find the height of the tower.

Answer 1

So

• tanØ=Perpendicular/Base

Height is perpendicular

• tan45=perpendicular/200
• perpendicular=200tan45
• perpendicular=200ft

Answer 2

Solution given:

Let AB be distance between tower ,angle of elevation be<A and height of tower be BC.

we have

<A=45°

AB=200ft

BC=?

Relationship between base and perpendicular is given by tan angle.

tan A=
`(perpendicular )/(base)`

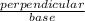
tan 45°=
`(BC )/(AB)`

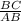
1=
`(BC )/(200ft)`

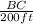
doing crisscrossed multiplication

BC=200ft

the height of the tower is 200ft.