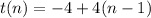Question

Choose the correct equation for an arithmetic

sequence in which t(4) = 8 and t(10) = 32
-

Answer 1

The equation is
`t(n) = -4 + 4(n-1)`

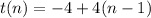
Explanation:

Arithmetic sequence:

In an arithmetic sequence, the difference between consecutive terms, called common difference, is always the same.

The general equation for an arithmetic sequence is:

`t(n) = t(1) + d(n-1)`

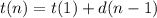
Taking the mth term as reference, the equation can be written as:

`t(n) = t(m) + d(n-m)`

t(4) = 8 and t(10) = 32

The common difference can be found:

`t(n) = t(m) + d(n-m)`

`t(10) = t(4) + d(10-4)`

`6d = 24`

`d = (24)/(6) = 4`

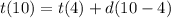
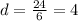
So

`t(n) = t(1) + 4(n-1)`

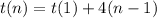
Finding the first term:

`t(4) = t(1) + 4(n-1)`

So

`t(1) = t(4) - 12 = 8 - 12 = -4`

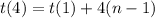
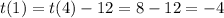
So

The equation is
`t(n) = -4 + 4(n-1)`