Question

the third term of an arithmetic series is 70 and the sum of the first 10 terms of the series is 450 . Calculate the common difference of the series .The sum of the series is Sn .Given that Sn > 350 . Find the set of possible values of n

Answer 1

Common difference is 6

Possible values of n is n > 8

Explanation:

(i) The nth term (Uₙ) of an arithmetic series is given by

Uₙ = a + (n-1)d --------------------(i)

and the sum of the series is given by;

Sₙ =
`(n)/(2)`(2a + (n-1)d) ---------------------(ii)

Where;

a = first term of the series

d = common difference of the series

n = the term or number of terms to be added.

Interpret the first statement

The third term of the series is 70. i.e

n = 3

Uₙ = U₃ = 30

Substitute these values into equation (i) as follows;

=> 30 = a + (3 - 1)d

=> 30 = a + 2d

=> a = 30 - 2d --------------------(iii)

Interpret the next statement

the sum of the first 10 terms of the series is 450. i.e

n = 10

Sₙ = S₁₀ = 450

Substitute these values into equation (ii) as follows:

=> 450 =
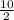`(10)/(2)`(2a + (10-1)d)

=> 450 = 5(2a + 9d)

Divide both sides by 5

=> 90 = 2a + 9d ---------------------------(iv)

Solve equations (iii) and (iv) simultaneously

Substitute the value of a in equation(iii) into equation (iv) and solve as follows

=> 90 = 2(30 - 2d) + 9d

=> 90 = 60 - 4d + 9d

=> 90 = 60 + 5d

=> 5d = 90 - 60

=> 5d = 30

Divide both sides by 5

=> d = 6

Therefore, the common difference, d is 6

(ii) Given

Sₙ > 350

From equation (ii), this implies that,

`(n)/(2)`(2a + (n-1)d) > 350 -------------------(v)

Let's get the value of the first term 'a'

Substitute the value of d = 6 into equation (iii) and solve as follows

=> a = 30 - 2(6)

=> a = 30 - 12

=> a = 18

Substitute the values of a and d into inequality (v) and solve

`(n)/(2)`(2(18) + (n-1)6) > 350

`(n)/(2)`(36 + 6n - 6) > 350

`(n)/(2)`(36 - 6 + 6n) > 350

`(n)/(2)`(30 + 6n) > 350

Multiply both sides by 2

n(30 + 6n) > 700

30n + 6n² > 700

6n² + 30n > 700

Divide through by 2

3n² + 15n > 350

3n(n+5) > 350

Solve the quadratic inequality

Since n specifies the number of terms to be added, it will always be a whole number. Therefore, using trial and error method, the values of n that will satisfy the above inequality will be values greater than 8. i.e

n > 8

In other words, for all values of n greater than 8, the above inequality will be satisfied.