Question

Please help worth 50points!!
Correct answers only please

Answer 1

Answers:

1. Choice D
2. Choice C
3. Choice C
4. Choice D
5. Choice B

===================================================

Explanations:

Problem 1

v = 9i - 4j means we move 9 units to the right and 4 units down.

Another way to write this is v = <9, -4>

----------------------

Problem 2

R = (-19, 6)

S = (-35, 13)

Subtract x coordinates: xS - xR = -35 - (-19) = -16

Subtract y coordinates: yS - yR = 13 - 6 = 7

Those results form the vector v = -16i + 7j

This vector indicates we move 16 units left and 7 units up when going from point R(-19,6) to point S(-35,13).

----------------------

Problem 3

t = -5i + 12j

||t|| = sqrt( (-5)^2 + (12)^2 )

||t|| = 13

theta = arctan(12/(-5))

theta = -67.38

Add on 180 to get to the proper quadrant Q2

-67.38 + 180 = 112.62

Therefore,

`t = 13\bigg\langle \cos(112.62^(\circ)), \ \sin(112.62^(\circ))\bigg\rangle`

----------------------

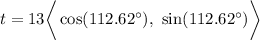
Problem 4

The x, y components are the coefficients of the linear form.

This allows us to go immediately from <-39,16> to -39i + 16j

----------------------

Problem 5

P = (-5,11)

Q = (-16,4)

Subtract x coords: xQ - xP = -16 - (-5) = -11

Subtract y coords: yQ - yP = 4 - 11 = -7

The component form of vector t is <-11, -7> and this vector is in Q3.

r = sqrt(a^2 + b^2)

r = sqrt( (-11)^2 + (-7)^2 )

r = 13.038 is the approximate length of the vector.

theta = arctan(b/a)

theta = arctan(-7/(-11))

theta = 32.471

Add on 180 so we get to Q3

32.471+180 = 212.471

Therefore, we have

`x = r\cos(\theta) = 13.038\cos(212.471^(\circ))\\\\y = r\sin(\theta) = 13.038\sin(212.471^(\circ))\\\\t = xi + yj\\\\t = 13.038\cos(212.471^(\circ))*i + 13.038\sin(212.471^(\circ))*j\\\\`

in which you could write into this slightly more compact form

`t = 13.038\bigg\langle\cos(212.471^(\circ)),\sin(212.471^(\circ))\bigg\rangle\\\\`

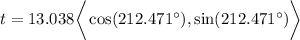
For more info, check out polar to cartesian conversion formulas.