Question

Help me solve this please

Answer 1

2384

Explanation:

1. Approach

To solve for the area of the given figure, divide the figure up into two parts. This will ensure that one can find the area of each individual part, and then add the two resulting areas up to find the total area of the figure. One can split this figure into a rectangle, and a triangle.

2.Find the area of the rectangle

The rectangle will have the following dimensions,

(40) x (50)

To find the area of a rectangle, one will use the following formula,

(length) * (width) = (area)

Therefore, the area is the following,

(40) * (50) = 2000

3.Area of the triangle

3a. Approach

To find the area of a triangle, one will use Heron's formula. Herons' formula states the following,

`√(s(s-a)(s-b)(s-c))`

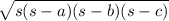
Where (s) is the semi-perimeter or half of the perimeter, and (a), (b), and (c) are the sides of the triangle. This requires that one knows all of the sides of the triangle.

3b. Find the unknown side and semi-perimeter

It is given that the triangle is right indicated by a box around one of the angles), thus one can use the Pythagorean theorem to find the length of the unknown side. The Pythagorean theorem states the following,

`a^2+b^2=c^2`

Where (a) and (b) represent the legs, the sides adjacent (next to) the right angle. Moreover, (c) represents the hypotenuse or the side opposite the right angle. Substitute in the given values and solve for (b),

`(40)^2=(24)^2+(b)^2\\`

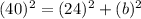
Simplify,

`1600=576+b^2`

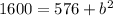
Inverse operations,

`1024=b^2\\√(1024)=b\\32=b`

Add up all of the sides of the triangle and divide by (2) to fin the semi-perimeter,

`(a+b+c)/(2)\\\\=(20+24+32)/(2)\\\\=48`

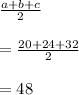
3c. Find the area of the triangle

Substitute into Heron's formula,

`√(s(s-a)(s-b)(s-c))\\\\=√(48(48-32)(48-40)(48-24))\\\\=√(48(16)(8)(24))\\\\=√(147456)\\\\=384`

Add the area of the rectangle and triangle together to find the answer,

384 + 2000

= 2384

Answer 2

2384

Explanation:

40x50=2000

40x24/2=384

2000+384=2384