Question

Given the Production Function Q = 72X + 15X 2 - X 3 , where Q =Output and X=Input (5 marks) a) What is the Marginal Product (MP) when X = 8? B) What is the Average Product (AP) when X = 6? C) At what value of X will Q be at its maximum? D) At what value of X will Diminishing Returns set in?

Answer 1

a.) Marginal Product (MP) = 120

b.) Average Product = 126

c.) At x = 12, the output is maximum.

d.) After 5 levels of inputs diminishing returns set in.

Explanation:

Given that,

Q = 72x + 15x² - x³

a.)

Marginal Product is equal to

`(dQ)/(dx) = 72 + 30x - 3x^(2)`

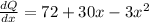
At x = 8

MP = 72 + 30(8) - 3(8)²

= 72 + 240 - 192

= 120

∴ we get

Marginal Product (MP) = 120

b.)

Average Product is equals to

=
`(Q)/(x)`

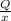
= 72 + 15x - x²

At x = 6

Average Product = 72 + 15(6) - 6²

= 72 + 90 - 36

= 126

∴ we get

Average Product = 126

c.)

For Maximizing Q,

Put
`(dQ)/(dx) = 0`

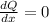
⇒72 + 30x - 3x² = 0

⇒24 + 10x - x² = 0

⇒x² - 10x - 24 = 0

⇒x² - 12x + 2x - 24 = 0

⇒x(x - 12) + 2(x - 12) = 0

⇒(x + 2)(x - 12) = 0

⇒x = -2, 12

As items can not be negative

∴ we get

At x = 12, the output is maximum.

d.)

Now,

For Diminishing Return

`(d(MP))/(dx) = (d^(2)Q)/(dx^(2) ) < 0`

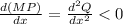
⇒30 - 6x < 0

⇒-6x < -30

⇒6x > 30

⇒x > 5

∴ we get

For x > 5, the diminishing returns set in

i.e.

After 5 levels of inputs diminishing returns set in.