Question

Smoke detectors fall into two major classes. Ionization detectors, the most common units, contain two parallel electrodes that are typically separated by 3 cm with a 5-V potential difference across them. The air molecules between the electrodes are ionized by collisions with helium nuclei that are produced by a radioactive source. Most units are initially fueled with 60 million nuclei of radioactive americium 241 (half-life 430 years). The now-ionized air molecules drift toward one of the electrodes with an average speed of 0.1 m/s and thus support a small current between the two electrodes. Smoke particles that enter and combine with the ions reduce the current and initiate an alarm.

Photoelectric detectors, by contrast, contain a light-emitting diode that sends a beam of unpolarized light across a small chamber. The light beam usually has a wavelength of 6.0 × 10–7m and has an intensity of 1.0 × 10–3 W. When smoke particles enter the chamber, the light scatters in all directions. A photocell then senses either the increase in the scattered light or the reduced intensity of the light beam and sets off the alarm. The speed of light in air is 3.0 × 108 m/s.
Ionization detectors respond faster to the large smoke particles of flaming fires; photoelectric detectors sense the small particles of smoldering fires more quickly. Modern units have both types of detectors.
When fewer than 3.75 × 106 americium nuclei remain, the ionization smoke detector will not operate due to insufficient ionization. How much time will pass before there are this many nuclei remaining?
a. 1720 years
b. 2150 years
c. 4300 years
d. 6880 years

Answer 1

1720 years is the amount of time that will pass.

Option a) 1720 years is the correct answer

Step-by-step explanation:

Given the data in the question;

Number of nuclei initially N₀ = 60 million = 60,000,000

After time t, Number of nuclei remaining N
`_{rem` = 3.75 × 10⁶

Also given that; half-life of radioactive americium
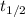`t_{1/2` = 430 years.

so;

λ = ln2 /
`t_{1/2`

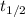
we substitute

λ = ln2 / 430 years

N
`_{rem` = N₀e^(-λt)

solve for t

t = 1/λ × ln( N₀/N
`_{rem` )

so we substitute

t = 1 / (ln2 / 430 years) × ln( 60,000,000 / ( 3.75 × 10⁶ ) )

t = ( 430 years / ln2 ) × ln( 60,000,000 / ( 3.75 × 10⁶ ) )

t = ( 430 years / 0.693147 ) × ln( 16 )

t = 620.359 years × 2.7725887

t = 1720.0003 ≈ 1720 years

Therefore, 1720 years is the amount of time that will pass.

Option a) 1720 years is the correct answer