Question

A person stands on level ground with both feet equidistant from each other directly under their shoulders. In this case, the normal force on each foot is...

A. equal to the force of gravity on the person.
B. greater than the force of gravity on the person.
C. equal to 1/2 the force of gravity on the person.
D. unrelated to the force of gravity on the person.

Answer 1

The correct option is C: the normal force of gravity on each foot is equal to 1/2 the force of gravity on the person.

Step-by-step explanation:

Since the feet are equidistant from each other, the total torque is zero:

`\Sigma \tau = 0`

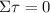
And the total forces acting on the feet are also equal to zero:

`\Sigma F = 0`

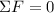
Hence, the normal force on the feet are:

`W = N_(1) + N_(2)`

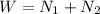
Where:

W: is the weight force

N₁: is the normal force of foot 1

N₂: is the normal force of foot 2

Since the normal force of each foot is the same, we have that N₁ = N₂ so:

`W = 2N`

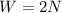
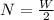`N = (W)/(2)` (1)

From the result of equation (1), we have that the normal force on each foot is equal to 1/2 the force of gravity on the person.

Therefore, the correct option is C: the normal force on each foot is equal to 1/2 the force of gravity on the person.

I hope it helps you!