Answer:
$ 251,619.37
Explanation:
Given that :
Loan = $ 268,000
Interest rate = 4.4 % per annum
4.4%/12 months = 0.366% per month
 :
:
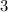 years to pay and
years to pay and
 years amortization
years amortization
 years x 12 months =
years x 12 months =
 months
months
Calculating the amount for he monthly amortization,
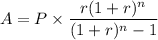


A = 1407.41
Therefore, the future value is given by :
![$FV=PV(1+r)^n-P\left[((1+r)^n-1)/(r)\right]$](https://img.qammunity.org/2022/formulas/mathematics/high-school/qa1lm6ud52flxlral2gy24exnqe85alqwt.png)
where, FV = future value ( balloon balance)
PV = present value (original balance)
P = payment
r = rate per payment
n = number of payments
![$FV=268,000(1+0.00366)^(36)-1407.41\left[((1+0.00366)^(36)-1)/(0.00366)\right]$](https://img.qammunity.org/2022/formulas/mathematics/high-school/5iyfelzoi3e7div73fwsg13sjltnhesyuw.png)
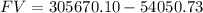
FV = 251619.37
Therefore, Stuart's balloon payment will be $ 251,619.37