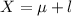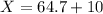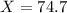Question

A 100 kg bungee jumper leaps from a bridge. The bungee cord has an un-streched equilibrium length of 10 m, and a spring constant of 35 N/m. What is the greatest vertical distance below the bridge surface that the bungee jumper will reach? Enter your answer as a positive number in meters, but do not enter units.

Answer 1

`X=74.7`

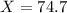
Step-by-step explanation:

From the question we are told that:

Mass
`m=100kg`

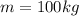
Length
`l=10m`

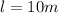
Spring constant
`\mu=35N/m`

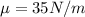
Generally the equation for potential energy of mass is mathematically given by

`P.E_m=mgh`

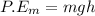
Since

`P.E_m=P.E_s`

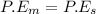
Where

P.E_s =potential energy of spring

Therefore

`m*g*(x+10) = 0.5*k*\mu^2`

`100*9.8*(x+10) = 0.5*35*\mu^2`

`980*(x+10) = 17.5*\mu^2`

`980*x+9800 = 17.5*\mu^2`

`17.5*\mu^2 - 980*\mu - 9800 = 0`

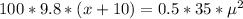
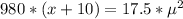
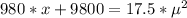
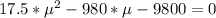
Comparing the equation above with standard quadratic equation

`17.5*\mu^2 - 980*\mu - 9800 = 0`

`ax^2+bx+c=0`

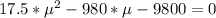
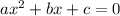
Giving

`a=17.5\\ b=-980\\ c=-9800`

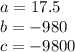
Solving Quadratic equation the roots of the equation is given as

`\mu_1=64.66`

`\mu_2=-8.661`

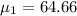
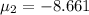
Since

`\mu` can not be -ve

Therefore

The vertical distance attained by the bungee jumper is given as

`X=\mu+l`

`X=64.7+10`

`X=74.7`

Answer 2

11.78meters

Step-by-step explanation:

Given data

Mass m = 100kg

Length of cord= 10m

Spring constant k= 35N/m

At the greatest vertical distance, the spring potential energy is equal to the gravitational potential energy

That is

Us=Ug

Us= 1/2kx^2

Ug= mgh

1/2kx^2= mgh

0.5*35*10^2= 100*9.81*h

0.5*35*100=981h

1750=981h

h= 1750/981

h= 1.78

Hence the bungee jumper will reach 1.78+10= 11.78meters below the surface of the bridge