Question

Trayectoria de un balón. El siguiente grafico ilustra la trayectoria d en balón de fútbol. La altitud máxima de recorrido del balón respecto al suelo es de 9m. Durante su ascenso ¿a qué distancia horizontal de su punto de partida el balón alcanza una altura de 7m. Durante el descenso.¿a qué distancia del punto de partida vuelve a estar a esa altura?

A) Ascenso 6,34; descenso 18m.

B)Ascenso 6.0m; descenso 17,66m.

C)Ascenso 6,34; descenso 17,66 m.

D) Ascenso 6m; descenso 18.

Proceso porfas ♡

Answer 1

C) Ascenso 6,34 m; Descenso 17,66 m

Explanation:

La altitud máxima que recorre la pelota con respecto al suelo, h = 9 metros

La forma general de la ecuación de una parábola es y = a·x² + b·x + c

La velocidad vertical inicial de la pelota,
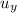`u_y` = √(2·g·h)

∴
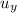`u_y` = √(2 × 9.81 × 9) ≈ 13.288

La velocidad vertical inicial de la pelota,
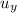`u_y` ≈ 13.288 m/s

El tiempo de vuelo de la pelota = 2 ×
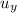`u_y`/g ≈ 2 × 13.288/9.81 = 2.709

El tiempo que tarda el balón en alcanzar los 7 metros sobre el suelo se indica de la siguiente manera;

s =
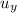`u_y`·t + (1/2)·g·t²

∴ 7 ≈ 13.288·t - (1/2)×9.81×t²

13.288·t - (1/2)×9.81×t² - 7 ≈ 0

Factorizar con el uso de una calculadora gráfica da;

t ≈ 0.716 s, or t ≈1.993t

Dado que la velocidad horizontal es constante, verificamos entre las opciones dadas una que proporcione los valores de la velocidad horizontal, vₓ, tanto para el ascenso como para el descenso, es decir, para ambos valores de 't' de la siguiente manera;

De las opciones de respuesta dadas, la velocidad horizontal es aproximadamente constante para la única opción 'C', donde tenemos;

vₓ = 6.34/0.716 ≈ 8.85

vₓ = 17.66/1.993 ≈ 8.86

El rango horizontal, d = 8.85 × 2.709 ≈ 24

La distancia horizontal de la pelota durante el ascenso cuando la pelota alcanza una altura de 7 m = 6.34 m, durante el descenso, la distancia horizontal = 17.66 m

La ecuación de una parábola (la trayectoria de la pelota) se puede presentar de la siguiente manera;

y = a·(x - h)² + k

Dónde;

(h, k) = La coordenada del vértice

k = 9

En el origen, (x, y) = (0, 0)

Por lo tanto;

0 = a · (0 - h) ² + 9

a · h² = -9

En y = 7. x = 6.34

∴ 7 = a · (6.34 - h) ² + 9

a = -2 / ((6,34 - h) ²)

a = -2 / ((17,66 - h) ²)

(6,34 - h) ² = (17,66 - h) ²

h²-12,68 · h + 40,1956 = h² -35,32 · h +311,8756

h² -35,32 · h + 311,8756 - (h²-12,68 · h + 40,1956) = 0

-35,32 · h + 12,68 · h = 40,1956 - 311,8756

h = (40,1956 - 311,8756) / (- 35,32 + 12,68)

a = -2 / ((6,34 - 12) ²) ≈ -0,06243054601

La trayectoria de la pelota es y = -0.06243054601 · (x - 12) ² + 9

Por tanto, la mejor opción correcta que cumpla con los parámetros dados es la opción C) Ascenso 6,34 m; Descendencia 17.66 m.