Question

A collection of 30 gems, all of which are identical in appearance, are supposedto be genuine diamonds, but actually contain 8 worthless stones. The genuine diamonds arevalued at $1200 each. Two gems are selected.

(a) Let X denote the total actual value of the gems selected. Find the probability distribution function for X.
(b) Find E(X).

Answer 1

Explanation:

From the given information:

There are 30 collections of gems, of which 8 are worthless;

Thus, the number of the genuine diamonds = 30 - 8 = 22.

Let X = random variable;

X consider the value as 0 (for 2 worthless stone selection),

X = 1200(1 worthless stone & 1 genuine stone)

X = 2400 (2 genuine stones selected)

However, the numbers of ways of selecting and chosen Gems can be estimated as:

`(^n_r) = (^(30)_2) \\ \\ \implies (30!)/(2!(30-2)!) \\ \\ \implies (30!)/(2!(28)!) \\ \\ \implies (30*29*28!)/(2!(28)!) \\ \\ \implies (30*29)/(2*1) \\ \\ \implies 435`

Thus;

`Pr (X = 0) = ((^8_2))/(435)`

`Pr (X = 0) = ((8!)/(2!(8-2)!))/(435) \\ \\ Pr (X = 0) = ((8!)/(2!(6)!))/(435) \\ \\ Pr (X = 0) = ((8*7*6!)/(2!(6)!))/(435) \\ \\ Pr (X = 0) = ((8*7)/(2*1))/(435) \\ \\ Pr (X = 0) = 0.0644`

`P(X =1200) = ((^(8)_(1))(^(22)_(1)))/(435)`

`P(X =1200) = ( (8!)/(1!(8-1)!)) ( (22!)/(1!(22-1)!)) )/(435)`

`P(X =1200) = ( (8) ( 22) )/(435)`

`P(X =1200) =0.4046`

`Pr (X = 2400) = ((^(22)_2))/(435)`

`Pr (X = 2400) = ((22!)/(2!(22-2)!))/(435) \\ \\ Pr (X = 2400) = ((22!)/(2!(20)!))/(435) \\ \\ Pr (X = 2400) = ((22*21*20!)/(2!(20)!))/(435) \\ \\ Pr (X =2400) = ((22*21)/(2*1))/(435) \\ \\ Pr (X = 2400) = 0.5310`

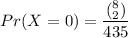
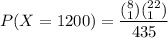
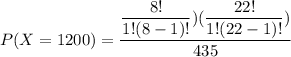
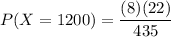
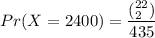
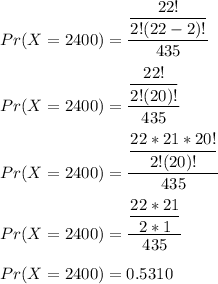
To find E(X):

E(X) = (0 × 0.0644) + (1200 × 0.4046) + (2400 × 0.5310)

E(X) = 0 + 485.52 + 1274.4

E(X) = 1759.92