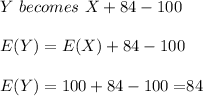Question

Suppose an agent has $100. He opens a demand deposit of S100 with a bank which has asset x where x is a random variable.

Required:
a. Suppose x is uniformly distributed on the interval [100, 200]. The density of x is f(x)=1/100 on [100,200] and f(x)=0 otherwise. What is the expected loss of the depositor?
b. Suppose changes in the economy changes the distribution of x. Now x is uniformly distributed on the interval [60, 200]. The density of x is f(x)=1/140 on [60, 200) and f(x)=0 otherwise. What is the expected loss of the depositor?
c. Suppose x is uniformly distributed on the interval [0, 200]. The density of x is f(x)=1/200 on [0, 200] and f(x)=0 otherwise. Calculate the expected loss of the depositor.
d. Suppose x is uniformly distributed on the interval [0, 200]. Given the macroeconomic environment, the government introduces deposit insurance. There is deposit insurance of an amount I=84. Calculate the expected loss of the depositor.

Answer 1

Following are the solution to the given points:

Step-by-step explanation:

Any agent has a $100 deposit to an institution of assets X to make a demand deposit of $100.

For point a:

`X \approx U(100,200)\\\\E(X) = ((100+200))/(2) = 150\\\\`

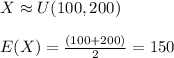
assume Y is the Loss of depositor

`Y = X - 100\\\\E(Y) = 150 - 100\\\\`

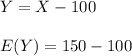
The expected loss of depositors
`E(Y) = \$50`

For point b:

`X \approx U(60,200)\\\\E(X) = ((60+200))/(2) = 130\\\\Y = X - 100\\\\E(Y) = 130 - 100\\`

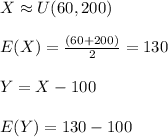
The expected loss of depositors
`E(Y) = \$30`

For point C:

`X \approx U(0,200)\\\\E(X) = ((0+200))/(2) = 100\\\\Y = X - 100\\\\E(Y) = 100 - 100`

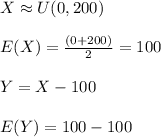
The expected loss of depositors
`E(Y) = \$0`

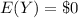
For point D:

`X \approx U(0,200)\\\\E(X) = ((0+200))/(2) = 100\\`

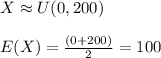
Here the government introduce deposits insurance, deposit insurance amount (I) is 84

`Y \ becomes\ X+84 - 100\\\\E(Y) = E(X) + 84 -100\\\\E(Y) = 100 + 84 -100= $84`