Question

NASA is giving serious consideration to the concept of solar sailing. A solar sailcraft uses a large, lowmass sail and the energy and momentum of sunlight for propulsion.

a. Should the sail be absorbing or reflective? Why?
b. The total power output of the sun is 3.9×10^26W. How large a sail is necessary to propel a 10,000-kg spacecraft against the gravitational force of the sun? Express your result in square kilometers.
c. Explain why your answer to part (b) is independent of the distance from the sun.

Answer 1

a) the reflective surface has twice the energy transfer

b) A = 1.3 10²⁷ km²

c) the energy emitted by the sun is distributed in a sphere that depends on the square of the distance, and the gravitational force depends on the square of the distance

Step-by-step explanation:

a) The pressure exerted on the candle is related to the variation of the momentum

P =
`(1)/(c) \ (dp)/(dt)`

in a case of absorption (inelastic shock) all the energy is absorbed therefore the pressure is

P = \frac{1}{c} \ \frac{dp}{dt}

in the case of reflection (elastic shock) an energy is absorbed by absorbing the light and then by action and reaction the same energy is absorbed in the reflected light

P = 2 \frac{1}{c} \ \frac{dp}{dt}

In conclusion, the reflective surface has twice the energy transfer.

b) pressure is defined with force per unit area

P = F / A

F = P A

this force must be greater than the gravitational force of attraction of the sun

Fg = G m Ms / r²

let's look for the case that the two forces are equal

F = Fg

P A_sail = G m Ms = r²

suppose a fully reflective sail

`2 (S)/(c) \ A_(sail) = G (m M_s)/(r^2)`

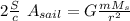
The pointing vector is the power delivered per unit area

S = I = P / A

where A is the area of ​​the sphere where the is distributed by the sun

A = 4π r²

we substitute

`(2P)/(c) \ (A_(sail))/(4 \pi r^2) = G (m M_s)/(r^2)`

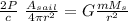
`(1)/(2 \pi \ c )` A_{sail} = G m M_s

A = G m M_s 2π c

let's calculate

A = 6.67 10⁻¹¹ 10000 2 10³⁰ 2π 3 10⁸

A = 1,257 10³³ m²

let's reduce to km²

A = 1.3 10³³ m² (1km / 10³ m) ²

A = 1.3 10²⁷ km²

c) The size of the candle is independent of the distance to the sun because the energy emitted by the sun is distributed in a sphere that depends on the square of the distance, and the gravitational force depends on the square of the distance, therefore the two dependencies are canceled.