Question

The equilibrium constant, Kp, for the following reaction is 0.636 at 600K.

COCl2(g) <=> CO(g) + Cl2(g)

If an equilibrium mixture of the three gases in a 16.9 L container at 600K contains COCl2 at a pressure of 0.836 atm and CO at a pressure of 0.551 atm, the equilibrium partial pressure of Cl2 is ............ atm.

Answer 1

Answer: The equilibrium partial pressure of
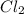`Cl_(2)` is 0.964 atm.

Step-by-step explanation:

Given:
`K_(p) = 0.636`

`P_{COCl_(2)} = 0.836 atm`

`P_(CO) = 0.551 atm`

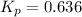
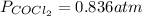
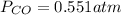
The given reaction equation is as follows.

`COCl_(2)(g) \rightleftharpoons CO(g) + Cl_(2)(g)`

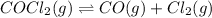
Formula used to calculate the partial pressure of
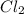`Cl_(2)` is as follows.

`K_(p) = \frac{P_(CO) * P_{Cl_(2)}}{P_{COCl_(2)}}`

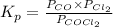
Substitute the values into above formula as follows.

`K_(p) = \frac{P_(CO) * P_{Cl_(2)}}{P_{COCl_(2)}}\\0.636 = \frac{0.551 atm * P_{Cl_(2)}}{0.836 atm}\\P_{Cl_(2)} = 0.964 atm`

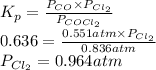
Thus, we can conclude that the equilibrium partial pressure of
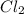`Cl_(2)` is 0.964 atm.