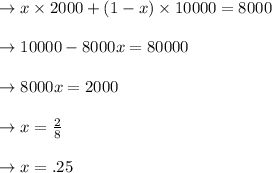Question

Consumers know that some fraction of all new cars produced and sold in the market are defective. The defective ones cannot be identified except by those who own them. Assume that cars do not depreciate in value with use. Suppose consumers are risk-neutral and value non-defective cars at $10,000 each and defective cars at $6,000 each. New cars sell for $8,000 and used ones for $2,000. (Note that since buyers are risk-neutral, the price of a new car reflects the expected value of purchasing a car that may or may not be defective.)

Required:
What is the fraction x?

Answer 1

The answer is "0.25".

Step-by-step explanation:

As buyers rate non-default cars at $10,000, we assume that almost all faulty cars are used. The reason would be that the automobiles have been priced at 2000$, which is well below a good 10000 dealer invoice, implying that only faulty products are available as old cars.

Some used cars sell at $2000, however, in the eyes of a buyer means a faulty vehicle.

Its price that even a threat customer is ready to pay was its price of a non-default product for a new car. It implies $8000 for a good car* chances that even a bad car will get a good car*chance*chances that even a bad car will get a bad one. Because people are aware which x part of all market vehicles is faulty, which means the fraction of good cars is 1-x. Enter beliefs, we get.

`\to x* 2000+(1-x)*10000=8000\\\\ \to10000-8000x=80000\\\\\to 8000x=2000\\\\\to x=(2)/(8)\\\\ \to x=.25`