Question

Records indicate that the daily high January temperatures on a tropical island tend to have a uniform distribution over the interval from 75°F to 90°F. A tourist arrives on the island on a randomly selected day in January.

a. What is the probability that the temperature will be above 80°F
b. What is the probability that the temperature will be between 80°F and 85°F 
c. What is the expected temperature?

Answer 1

a) 0.6667 = 66.67% probability that the temperature will be above 80°F.

b) 0.3333 = 33.33% probability that the temperature will be between 80°F and 85°F.

c) The expected temperature is of 82.5ºF.

Explanation:

Uniform distribution:

The probability of all outcomes between a and b is the same.

Uniform distribution over the interval from 75°F to 90°F.

This means that
`a = 75, b = 90`

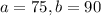
a. What is the probability that the temperature will be above 80°F?

We have that, on the uniform distribution:

`P(X > x) = (b - x)/(b - a)`

In this question:

`P(X > 80) = (90 - 80)/(90 - 75) = (10)/(15) = 0.6667`

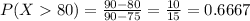
0.6667 = 66.67% probability that the temperature will be above 80°F.

b. What is the probability that the temperature will be between 80°F and 85°F?

We have that:

`P(c \leq X \leq d) = (d - c)/(b - a)`

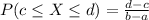
Then, in this question:

`P(80 \leq X \leq 85) = (85 - 80)/(90 - 75) = (5)/(15) = 0.3333`

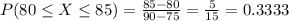
0.3333 = 33.33% probability that the temperature will be between 80°F and 85°F.

c. What is the expected temperature?

The expected value of the uniform distribution is:

`E = (a + b)/(2)`

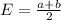
In this question:

`E = (75 + 90)/(2) = 82.5`

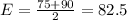
The expected temperature is of 82.5ºF.