Question

Expedia would like to test the hypothesis that the proportion of Southwest Airline flights that arrive on-time is less than 0.90. A random sample of 140 United Airline flights found that 119 arrived on-time. Expedia would like to set α = 0.05. The conclusion for this hypothesis test would be that because the test statistic is ____________________________________________.

a. more than the critical value, we can conclude that the proportion of United Airline flights that arrive on-time is more than 0.90
b. more than the critical value, we cannot conclude that the proportion of United Airline flights that arrive on-time is less than 0.90
c. less than the critical value, we can cannot conclude that the proportion of United Airline flights that arrive on-time is less than 0.90
d. less than the critical value, we can conclude that the proportion of United Airline flights that arrive on-time is less than 0.90

Answer 1

d. less than the critical value, we can conclude that the proportion of United Airline flights that arrive on-time is less than 0.90

Explanation:

Expedia would like to test the hypothesis that the proportion of Southwest Airline flights that arrive on-time is less than 0.90.

At the null hypothesis, we test that the proportion is of 0.9, that is:

`H_0: p = 0.9`

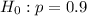
At the alternate hypothesis, we test that it is less than 0.9, that is:

`H_a: p < 0.9`

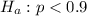
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.9 is tested at the null hypothesis:

This means that
`\mu = 0.9, \sigma = √(0.9*0.1)`

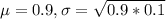
A random sample of 140 United Airline flights found that 119 arrived on-time.

This means that
`n = 140, X = (119)/(140) = 0.85`

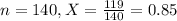
Value of the test-statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.85 - 0.9)/((√(0.9*0.1))/(√(140)))`

`z = -1.97`

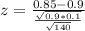
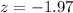
P-value of the test and decision:

The p-value of the test is the probability of finding a sample proportion of 0.85 or less, which is the p-value of z = -1.97.

Looking at the z-table, z = -1.97 has a p-value of 0.0244.

The p-value is 0.0244 < 0.05, which means that the test statistic is less than the critical value, and thus, we can conclude that the proportion of United Airline flights that arrive on-time is less than 0.90.

The correct answer is given by option d.