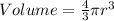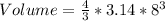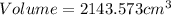Answer:

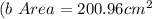
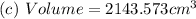
Explanation:
The largest cross-section of a sphere is the center.
So, we have:
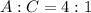
Where
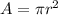
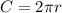
Solving (a): The radius
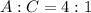 implies that
implies that
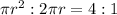
Express as fraction

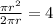
Divide by

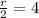
Make r the subject
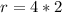
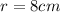
Solving (b): Area of the largest cross-section.
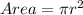
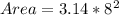

Solving (b): Volume of the sphere