Question

Magnetic resonance imaging often need magnetic fields of a strength of around 1.50 T. The solenoid is 1.80 meters long and 75.0 cm in diameter. It is tightly wound with a single layer of 2.00 mm diameter superconducting wire.

Required:
What current is needed?

Answer 1

The current needed is 2387.32 A

Step-by-step explanation:

Given;

strength of the magnetic field, B = 1.5 T

length of the solenoid, L = 18 m

diameter of the solenoid, D = 75 cm = 0.75 m

diameter of the superconducting wire, d = 2 mm = 0.002 m

The number of turns of the solenoid is calculated as;

`N = (length \ of \ solenoid)/(diameter \ of \ wire ) = (1.8)/(0.002) = 900 \ turns`

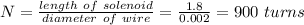
The magnetic field strength is given by;

`B = (\mu_0 NI)/(L) \\\\`

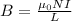
Where;

I is the current needed

μ₀ is permeability of free space = 4π x 10⁻⁷ T.m/A

`I = (BL)/(\mu_0 N) =(1.5 * 1.8)/(4\pi * 10^(-7) \ * 900) \\\\I = 2387.32 \ A`

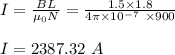
Therefore, the current needed is 2387.32 A