Question

A new fast food restaurant wants to start deliver food. The owner of the store has determined that home delivery will be successful if the average time spent on the deliveries does not exceed 24 minutes. The owner has randomly selected 32 customers and has delivered food to their homes. The mean delivery time for the sample is 26 minutes with standard deviation of 5.8 minutes. Test if the mean delivery time actually exceeds 24 minutes.

Required:
a. Give the null and alternative hypotheses to determine if the mean delivery time actually exceeds 24 minutes.
b. Calculate the test statistics.
c. At α=0.05, which of the following conclusion is correct?

1. At α=0.05, there is no sufficient evidence to conclude that the mean delivery time exceed 24 minutes.
2. At α=0.05, there is sufficient evidence to conclude the mean delivery time exceeds 24 minutes.
3. At α=0.05, there is sufficient evidence to conclude the mean delivery time less 24 minutes.
4. At α=0.05, there is sufficient evidence to conclude that the mean delivery time is 24 minutes

Answer 1

a.

The null hypothesis is
`H_0: \mu \leq 24`.

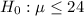The alternate hypothesis is
`H_1: \mu > 24`.

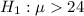b.

The test statistic is
`t = 1.95`

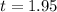
c.

2. At α=0.05, there is sufficient evidence to conclude the mean delivery time exceeds 24 minutes.

Explanation:

Question a:

Test if the mean delivery time actually exceeds 24 minutes.

At the null hypothesis, we test that the mean is of 24 minutes or less, that is:

`H_0: \mu \leq 24`

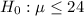
At the alternate hypothesis, we test if it is more, that is:

`H_1: \mu > 24`

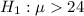
Question b:

We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.

The test statistic is:

`t = (X - \mu)/((\sigma)/(√(n)))`

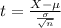
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`s` is the standard deviation of the sample and n is the size of the sample.

24 is tested at the null hypothesis:

This means that
`\mu = 24`

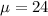
The owner has randomly selected 32 customers and has delivered food to their homes. The mean delivery time for the sample is 26 minutes with standard deviation of 5.8 minutes.

This means that
`n = 32, X = 26, s = 5.8`.

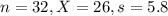Value of the test-statistic:

`t = (X - \mu)/((\sigma)/(√(n)))`

`t = (26 - 24)/((5.8)/(√(32)))`

`t = 1.95`

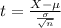
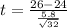
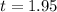
The test statistic is
`t = 1.95`.

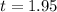c. At α=0.05, which of the following conclusion is correct?

The p-value of the test is the probability of finding a sample mean above 26, which is a right-tailed test of t = 1.95 with 32 - 1 = 31 degrees of freedom.

Using a t-distribution calculator, this p-value is of 0.0301.

Since the p-value is 0.0301 < 0.05, there is sufficient evidence to conclude the mean delivery time exceeds 24 minutes, and the correct answer is given by option 2.