Question

A woman has eight keys on a key ring, one of which fits the door she wants to unlock. Sherandomly selects a key and tries it. If it does not unlock the door, she randomly selects anotherkey from those remaining and tries to unlock the door with it. She continues in this manner untilthe door is unlocked. Let X be the number of keys she tries before unlocking the door, countingthe key that actually worked.

Required:
Find the expected number of keys she will try before she opens the door.

Answer 1

The expected number of keys she will try before she opens the door is 4.5.

Explanation:

A woman has eight keys on a key ring, one of which fits the door she wants to unlock.

Each of them is equally as likely to be the one to work, which means that this situation is represented by an uniform distribution with lower bound
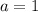`a = 1` and upper bound
`b = 8`.

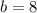Find the expected number of keys she will try before she opens the door.

The expected value of the uniform distribution is given by:

`E = (a + b)/(2)`

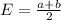
Considering
`a = 1, b = 8`, as is the case in this exercise:

`E = (1 + 8)/(2) = 4.5`

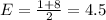
The expected number of keys she will try before she opens the door is 4.5.