Answer:
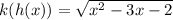
![x = (\infty, -0.56]\ u\ [3.56, \infty)](https://img.qammunity.org/2022/formulas/mathematics/college/huer1t0dy9svhruid7b73ipx42m8mbiyvp.png)
Explanation:
Given
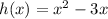
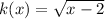
Solving (a): k(h(x))
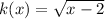
Replace x with h(x)
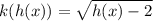
Substitute:
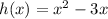
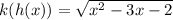
Solving (b): The domain
For the function to be defined, the expression in the root must be greater than or equal to 0; i.e.
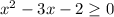
Solve for x;
Using a calculator, we have:
 and
and
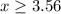 --- approximated
--- approximated
So, the domain is:
![x = (\infty, -0.56]\ u\ [3.56, \infty)](https://img.qammunity.org/2022/formulas/mathematics/college/huer1t0dy9svhruid7b73ipx42m8mbiyvp.png)