Question

A 2 kg cart is held onto a spring (1,037 N/m) and is compressed 1.1 m. The cat is

released and travels up a hill. At the top of the hill the cart is traveling at 4 m/s, how
much energy is converted to gravitational energy?

Answer 1

611.385 joules are converted to gravitational potential energy.

Step-by-step explanation:

Let suppose that the cart begins at a height of 0 meters. The cart-spring system is conservative. By the Principle of Energy Conservation we have the following model:

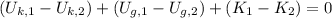`(U_(k,1)-U_(k,2)) + (U_(g,1)-U_(g,2)) + (K_(1)-K_(2)) = 0` (1)

Where:

`U_(k,1)`,
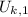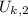`U_(k, 2)` - Initial and final elastic potential energy, in joules.

`U_(g,1)`,
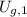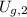`U_(g,2)` - Initial and final gravitational potential energy, in joules.

`K_(1)`,
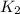`K_(2)` - Initial and final translational kinetic energy, in joules.

And the energy converted to gravitational potential energy is calculated by (1) and definitions of translational kinetic and elastic potential energies:

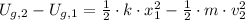`U_(g,2) - U_(g,1) = (1)/(2)\cdot k\cdot x_(1)^(2) - (1)/(2)\cdot m\cdot v_(2)^(2)` (2)

Where:

`k` - Spring constant, in newtons per meter.

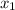`x_(1)` - Initial compression of the spring, in meters.

`m` - Mass, in kilograms.

`v_(2)` - Final speed of the cart, in meters per second.

If we know that
`k = 1037\,(N)/(m)`,
`x_(1) = 1.1\,m`,
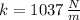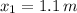`m = 2\,kg` and
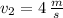`v_(2) = 4\,(m)/(s)`, then the change in gravitational potential energy is:

`U_(g,2) - U_(g,1) = (1)/(2)\cdot \left[\left(1037\,(N)/(m) \right)\cdot (1.1\,m)^(2) - (2\,kg)\cdot \left(4\,(m)/(s) \right)^(2)\right]`

`U_(g,2) - U_(g,1) = 611.385\,J`

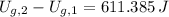
611.385 joules are converted to gravitational potential energy.