Answer:
The force that must be applied to maintain a constant velocity is equal o the friction force which is 2,650 N
The total force required from rest is (2,650·t + 20,972.
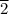 )/t N
)/t N
Step-by-step explanation:
The given data of the car in motion are;
The mass of the car, m = 1,510 kg
The force of friction from the road,
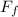 = 2,650 N
= 2,650 N
When the car is moving at 50.0 km/hr, we have;
v = 50.0 km/hr = 250/9 m/s ≈ 13.88889 m/s
According to Newton's first Law of motion, a body will continue in a state of rest or in uniform motion along a straight line unless acted on by a force
The force acting on the car in motion = 2,650 N
When the car is moving at a constant velocity, the forces acting on the car are in equilibrium and the net force is zero
Therefore;
The magnitude of the force that will keep the car moving at a constant velocity = The friction force of the road = 2,650 N
The direction of the force = In the direction of motion of the car
Where the time it takes the car to accelerate from rest to 50.0 km/hr = t seconds, we have;
The force required to move at a constant speed = 1,510 kg × (250/9 m/s - 0)/t s = 20,972.
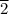 /t N
/t N
The total force required to move forward with a constant velocity of 50.0 km/hr becomes 20,972.
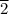 /t N + 2,650 N = (2,650·t + 20,972.
/t N + 2,650 N = (2,650·t + 20,972.
 )/t N
)/t N
Where;
t = The time it takes the car to reach 50.0 km/hr from rest.