Question

Find the LcM of 160, 192,240​

Answer 1

Given:

The numbers are 160, 192, 240​.

To find:

The LCM of 160, 192, 240.

Solution:

The given numbers are 160, 192, 240​. Write the factor forms of these numbers.

`160=2* 2* 2* 2* 2* 5`

`160=2^5* 5`

`192=2* 2* 2* 2* 2* 2* 3`

`192=2^6* 3`

`240=2* 2* 2* 2* 3* 5`

`240=2^4* 3* 5`

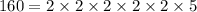
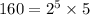
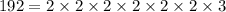
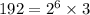
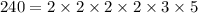
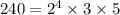
Now, the LCM of given numbers is the product of all prime factors with highest degrees.

`LCM=2^6* 3* 5`

`LCM=64* 15`

`LCM=960`

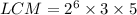
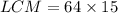
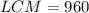
Therefore, the LCM of given numbers is 960.