Given:
The complex number is:
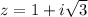
To find:
The argument of the given complex number.
Solution:
If a complex number is
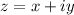 , then the argument of the complex number is:
, then the argument of the complex number is:
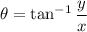
We have,
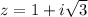
Here,
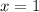 and
and
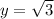 . So, the argument of the given complex number is:
. So, the argument of the given complex number is:
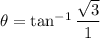
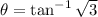
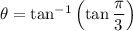
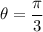
Therefore, the argument of the given complex number is
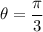 .
.