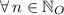Answer:
Amplitude:

Period:

Minimum: -4
Maximum: 4
Intercepts:
![x = (1)/(2)\cdot [0 \pm \pi \cdot n]](https://img.qammunity.org/2022/formulas/sat/high-school/g4tp4tyt727y33z0brpqy5exxl9i9hlsrr.png) ,
,
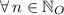
Step-by-step explanation:
The expression described on statement is a sinusoidal formula, whose expression is of the form:
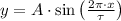 (1)
(1)
Where:
 - Independent variable.
- Independent variable.
 - Dependent variable.
- Dependent variable.
 - Amplitude.
- Amplitude.
 - Period.
- Period.
By direct comparison, we calculate the amplitude and period:
Amplitude

Period


Minimum and Maximum
The sine is a bounded function between -1 and 1, meaning that sinusoidal formula is bounded between
 and
and
 . Hence, the minimum and maximum are -4 and 4, respectively.
. Hence, the minimum and maximum are -4 and 4, respectively.
Intercepts
The intercepts are set of points of the sinusoidal formula such that
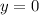 . The sine function is a periodic function which equals 0 each
. The sine function is a periodic function which equals 0 each
 radians.
radians.
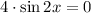
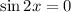
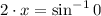
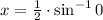
![x = (1)/(2)\cdot [0 \pm \pi \cdot n]](https://img.qammunity.org/2022/formulas/sat/high-school/g4tp4tyt727y33z0brpqy5exxl9i9hlsrr.png) ,
,