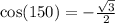Question

Show an example of how to evaluate a trigonometric function using reference

angle (without a calculator/ you may use left hand rule or unit circle)

Answer 1

`\cos(150) = -(\sqrt 3)/(2)`

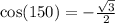
Step-by-step explanation:

An example is as follows;

Using reference angle, evaluate
`\cos(150)`

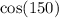
Solution:

We have:
`\cos(150)`

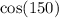
150 degrees is in the second quadrant, and it makes 30 degrees (i.e. 180 - 150) with the x-axis.

This implies that, cos(150) has the same magnitude as cos(30);

The only difference in the values is the sign; because

• 30 degrees is in the first quadrant where all functions are positive

• 150 degrees is in the third quadrant where all cosine is negative

So, we have:

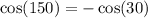
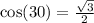
`\cos(150) = -\cos(30)`

-----------------------------------------------

`\cos(30) = (\sqrt 3)/(2)`

-----------------------------------------------

`\cos(150) = -(\sqrt 3)/(2)`