Question

On a standardized exam, the scores are normally distributed with a mean of 350 and

a standard deviation of 40. Find the Z-score of a person who scored 346 on the exam.

Answer 1

`\boxed {\boxed {\sf z= -0.1}}`

Explanation:

A z-score helps describe the relationship between a value and the mean of a group of values. Basically, it tells us how many standard deviations away from the mean a value is. The formula is:

`z= (x- \mu)/(\sigma)`

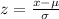
where x is the value, μ is the mean, and σ is the standard deviation.

For this standardized exam, the mean is 350 and the standard deviation is 40. We want to find the z-score for a value of 346.

• x= 346
• μ= 350
• σ= 40

Substitute the values into the formula.

`z= ( 346-350)/(40)`

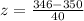
Solve the numerator.

`z- ( -4)/(40)`

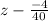
Divide.

`z= -0.1`

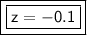
The z score is -0.1, so the person with a score of 346 on the exam was 0.1 standard deviations lower than the mean.