Question

A line has this equation: y = -8x + 8,

Write an equation for the parallel line that goes through (9,7)

Answer 1

Parallel lines have the same slope
Y = -8x + 8
The slope will be -8
Therefore: y = -8x + b
Plug in the point
7 = -8(9) + b
7 = -72 + b, b = 79

Solution: y = -8x + 79

Answer 2

hello!

`=======================================`

parallel lines have the same slope; it means that if we have a line with a slope of -8, then the line parallel to the given line has the same slope (-8)

now, we are also given a point that the line passes through:

(9, 7)

we can use point-slope form:

`\pmb{y-y1=m(x-x1)}`

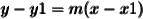
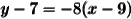`\pmb{y-7=-8(x-9)}` (point-slope form)

now, convert to slope-intercept form, if necessary:

`\pmb{y-7=-8x+72}`

`\pmb{y=-8x+72+7}`

`\pmb{y=-8x+79}`

`================================`

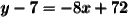
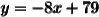
note:-

Hope everything is clear; if you need any more explanation, kindly let me know.