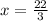Answer:
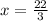
Explanation:
Since both CB and ED intersect AD perpendicularly, we can say they are parallel and that ΔACB is similar to ΔAED from Thales intercept theorem. Now, we can set up a proportion from the definition of similar triangles:
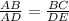
We can say that AD = AB + BD(segment addition postulate) and substitute to get AD = 11. Now we can plug in the numbers we have to the proportion:
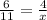
We can cross-multiply to get:
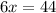
and divide by 6 to get