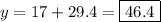Question

Can someone help me, please? I need to find the value of x and y rounded to the nearest tenth. Thank you!​

Answer 1

`x\approx 24.0,\\y\approx 46.4`

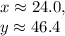
Explanation:

Let the height of the largest triangle marked be
`h`. We can set up the following equation:

`\sin 30^(\circ)=(h)/(34),\\h=34 \sin 30^(\circ)=17` (if you're unfamiliar with trig, this is likely introduced to you as 30-60-90 triangle rules)

This height is also a leg of a 45-45-90 triangle, as marked in the diagram. From the isosceles-base-theorem, the other leg of this triangle must also be equal to
`h`. Therefore, we can use the Pythagorean theorem to solve for
`x`:

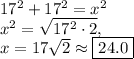`17^2+17^2=x^2\\x^2=√(17^2\cdot 2),\\x=17√(2)\approx \boxed{24.0}` (you can also use trig or 45-45-90 triangle rules which are derived from the Pythagorean theorem)

Segment
`y` consists of two shorter segments, a left segment and a right segment. We've already found that the left segment is equal to 17. To find the right segment we can use trig, the Pythagorean theorem, or 30-60-90 triangle rules (derived from the Pythagorean theorem):

Using Pythagorean Theorem:

`y_(right)=√(34^2-17^2)\approx \boxed{29.4}`

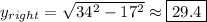
Therefore, we have:

`y=17+29.4=\boxed{46.4}`